What Is The Behavior Called That Maximizes An Animal's Energy Intake-to-expenditure Ratio

Behavioral ecology model

Worker bees forage nectar non but for themselves, just for their whole hive community. Optimal foraging theory predicts that this bee will provender in a way that volition maximize its hive's internet yield of energy.

Optimal foraging theory (OFT) is a behavioral ecology model that helps predict how an creature behaves when searching for food. Although obtaining nutrient provides the animal with energy, searching for and capturing the food require both energy and time. To maximize fitness, an beast adopts a foraging strategy that provides the nearly benefit (energy) for the lowest price, maximizing the net free energy gained. OFT helps predict the best strategy that an animal can utilize to achieve this goal.

OFT is an ecological application of the optimality model. This theory assumes that the well-nigh economically advantageous foraging design will be selected for in a species through natural choice.^[one] When using OFT to model foraging beliefs, organisms are said to be maximizing a variable known every bit the currency, such equally the almost nutrient per unit fourth dimension. In improver, the constraints of the environment are other variables that must be considered. Constraints are defined as factors that can limit the forager'southward ability to maximize the currency. The optimal decision rule, or the organism's best foraging strategy, is divers as the decision that maximizes the currency nether the constraints of the surroundings. Identifying the optimal decision dominion is the master goal of the Ofttimes.^[2]

Building an optimal foraging model [edit]

An optimal foraging model generates quantitative predictions of how animals maximize their fettle while they provender. The model building process involves identifying the currency, constraints, and appropriate decision rule for the forager.^{[2] [iii]}

Currency is defined as the unit that is optimized by the animal. It is also a hypothesis of the costs and benefits that are imposed on that animal.^[iv] For case, a sure forager gains free energy from food, simply incurs the cost of searching for the nutrient: the time and energy spent searching could have been used instead on other endeavors, such as finding mates or protecting young. It would be in the animal's best interest to maximize its benefits at the everyman toll. Thus, the currency in this situation could exist defined as net free energy gain per unit time.^[2] However, for a different forager, the time it takes to assimilate the food after eating could be a more significant cost than the time and energy spent looking for food. In this case, the currency could be defined as net free energy gain per digestive turnover time instead of cyberspace free energy gain per unit fourth dimension.^[5] Furthermore, benefits and costs tin can depend on a forager's community. For example, a forager living in a hive would well-nigh probable forage in a mode that would maximize efficiency for its colony rather than itself.^[iv] Past identifying the currency, i tin can construct a hypothesis nigh which benefits and costs are of import to the forager in question.

Constraints are hypotheses about the limitations that are placed on an beast.^[4] These limitations can be due to features of the surroundings or the physiology of the animal and could limit their foraging efficiency. The time that information technology takes for the forager to travel from the nesting site to the foraging site is an instance of a constraint. The maximum number of food items a forager is able to comport dorsum to its nesting site is some other example of a constraint. In that location could also be cerebral constraints on animals, such as limits to learning and memory.^[ii] The more constraints that one is able to identify in a given system, the more predictive ability the model will have.^[iv]

Effigy i. Energy gain per cost (East) for adopting foraging strategy x. Adapted from Parker & Smith.^[six]

Given the hypotheses near the currency and the constraints, the optimal conclusion rule is the model's prediction of what the creature's best foraging strategy should exist.^[2] Possible examples of optimal decision rules could be the optimal number of food items that an beast should carry back to its nesting site or the optimal size of a food item that an brute should feed on. Figure one, shows an case of how an optimal determination rule could be determined from a graphical model.^[6] The curve represents the energy gain per toll (Eastward) for adopting foraging strategy ten. Free energy gain per cost is the currency beingness optimized. The constraints of the system determine the shape of this curve. The optimal determination rule (x*) is the strategy for which the currency, energy gain per costs, is the greatest. Optimal foraging models can look very different and become very circuitous, depending on the nature of the currency and the number of constraints considered. Withal, the full general principles of currency, constraints, and optimal decision dominion remain the same for all models.

To test a model, one can compare the predicted strategy to the fauna's actual foraging beliefs. If the model fits the observed information well, then the hypotheses about the currency and constraints are supported. If the model doesn't fit the data well, then it is possible that either the currency or a particular constraint has been incorrectly identified.^[four]

Different feeding systems and classes of predators [edit]

Optimal foraging theory is widely applicable to feeding systems throughout the animal kingdom. Under the Often, any organism of interest can be viewed as a predator that forages prey. There are different classes of predators that organisms fall into and each class has distinct foraging and predation strategies.

• Truthful predators attack large numbers of casualty throughout their life. They kill their casualty either immediately or shortly afterward the assail. They may eat all or simply part of their prey. True predators include tigers, lions, whales, sharks, seed-eating birds, ants.^[7]
• Grazers eat but a portion of their prey. They harm the prey, only rarely kill information technology. Grazers include antelope, cattle, and mosquitoes.
• Parasites, like grazers, eat just a function of their casualty (host), merely rarely the unabridged organism. They spend all or large portions of their life cycle living in/on a single host. This intimate relationship is typical of tapeworms, liver flukes, and plant parasites, such every bit the potato blight.
• Parasitoids are mainly typical of wasps (social club Hymenoptera), and some flies (order Diptera). Eggs are laid inside the larvae of other arthropods which hatch and consume the host from the within, killing information technology. This unusual predator–host human relationship is typical of about 10% of all insects.^[8] Many viruses that assail single-celled organisms (such every bit bacteriophages) are too parasitoids; they reproduce inside a unmarried host that is inevitably killed by the association.

The optimization of these different foraging and predation strategies tin exist explained by the optimal foraging theory. In each instance, in that location are costs, benefits, and limitations that ultimately make up one's mind the optimal decision rule that the predator should follow.

The optimal diet model [edit]

Ane classical version of the optimal foraging theory is the optimal diet model, which is too known as the casualty choice model or the contingency model. In this model, the predator encounters dissimilar prey items and decides whether to eat what it has or search for a more assisting prey detail. The model predicts that foragers should ignore low profitability prey items when more profitable items are present and abundant.^[9]

The profitability of a prey item is dependent on several ecological variables. E is the corporeality of energy (calories) that a casualty particular provides the predator. Handling time (h) is the amount of fourth dimension information technology takes the predator to handle the food, beginning from the time the predator finds the prey detail to the time the casualty particular is eaten. The profitability of a prey detail is then divers equally East/h. Additionally, search fourth dimension (South) is the amount of fourth dimension it takes the predator to discover a casualty particular and is dependent on the affluence of the nutrient and the ease of locating it.^[2] In this model, the currency is energy intake per unit fourth dimension and the constraints include the actual values of E, h, and S, likewise as the fact that prey items are encountered sequentially.

Model of selection between big and small prey [edit]

Using these variables, the optimal diet model can predict how predators choose betwixt two prey types: large prey_one with energy value East₁ and handling fourth dimension h_one , and small-scale casualty₂ with energy value East₂ and treatment time h₂ . In order to maximize its overall rate of energy gain, a predator must consider the profitability of the two casualty types. If it is assumed that large prey₁ is more profitable than pocket-sized prey₂, then E_ane/h₁ > Eastward₂/h₂ . Thus, if the predator encounters casualty_i, it should always cull to consume it, considering of its college profitability. It should never carp to go searching for casualty₂. Nonetheless, if the beast encounters casualty₂, it should reject it to wait for a more assisting prey_i, unless the fourth dimension it would accept to find prey₁ is also long and costly for it to be worth it. Thus, the brute should consume prey_two only if East_two/h₂ > Eastward_i/(h₁+S₁), where Southward₁ is the search fourth dimension for prey_one. Since it is always favorable to choose to consume prey₁, the selection to eat prey₁ is non dependent on the affluence of casualty₂. Merely since the length of S₁ (i.eastward. how difficult it is to find prey1) is logically dependent on the density of prey_ane, the choice to eat casualty₂ is dependent on the abundance of prey_i.^[iv]

Generalist and specialist diets [edit]

The optimal nutrition model also predicts that unlike types of animals should prefer different diets based on variations in search fourth dimension. This idea is an extension of the model of prey pick that was discussed above. The equation, Due east_two/h₂ > E_i/(h₁+Southward_i), can be rearranged to give: S_one > [(E₁h₂)/East₂] – h_ane . This rearranged form gives the threshold for how long S_one must exist for an animal to cull to eat both prey_one and prey_ii.^[4] Animals that have Southward₁'southward that attain the threshold are defined as generalists. In nature, generalists include a wide range of prey items in their nutrition.^[ten] An example of a generalist is a mouse, which consumes a big variety of seeds, grains, and basics.^[xi] In contrast, predators with relatively brusque Due south_i'due south are still better off choosing to eat just prey₁. These types of animals are divers as specialists and have very exclusive diets in nature.^[10] An instance of a specialist is the koala, which solely consumes eucalyptus leaves.^[12] In general, dissimilar animals beyond the iv functional classes of predators exhibit strategies ranging beyond a continuum between being a generalist and a specialist. Additionally, since the selection to eat prey2 is dependent on the abundance of prey1 (equally discussed earlier), if prey1 becomes then scarce that S1 reaches the threshold, then the animal should switch from exclusively eating prey1 to eating both prey1 and prey2.^[4] In other words, if the food inside a specialist's diet becomes very scarce, a specialist can sometimes switch to being a generalist.

Functional response curves [edit]

Every bit previously mentioned, the amount of time it takes to search for a prey item depends on the density of the prey. Functional response curves evidence the charge per unit of prey capture every bit a function of food density and can be used in conjunction with the optimal nutrition theory to predict foraging behavior of predators. At that place are three dissimilar types of functional response curves.^[13]

Figure 2. Three types of functional response curves. Adjusted from Staddon.^[13]

For a Blazon I functional response curve, the rate of casualty capture increases linearly with nutrient density. At depression prey densities, the search time is long. Since the predator spends most of its time searching, it eats every casualty item it finds. Every bit prey density increases, the predator is able to capture the prey faster and faster. At a certain point, the rate of prey capture is so high, that the predator doesn't take to swallow every prey particular it encounters. Afterward this betoken, the predator should cull merely the prey items with the highest East/h.^[xiv]

For a Type Ii functional response curve, the rate of prey capture negatively accelerates every bit it increases with food density.^[thirteen] This is because it assumes that the predator is express by its capacity to process nutrient. In other words, equally the food density increases, treatment time increases. At the beginning of the curve, rate of prey capture increases nearly linearly with prey density and there is nigh no handling time. Every bit prey density increases, the predator spends less and less time searching for casualty and more and more time treatment the prey. The charge per unit of casualty capture increases less and less, until it finally plateaus. The high number of prey basically "swamps" the predator.^[14]

A Type III functional response bend is a sigmoid bend. The charge per unit of prey capture increases at commencement with casualty density at a positively accelerated rate, but so at high densities changes to the negatively accelerated course, similar to that of the Type II bend.^[thirteen] At high prey densities (the top of the curve), each new prey item is defenseless near immediately. The predator is able to exist finicky and doesn't eat every item it finds. And so, assuming that in that location are two prey types with different profitabilities that are both at high abundance, the predator will cull the item with the higher Due east/h. However, at low prey densities (the bottom of the curve) the charge per unit of prey capture increases faster than linearly. This ways that as the predator feeds and the prey type with the college Eastward/h becomes less abundant, the predator will start to switch its preference to the prey type with the lower Due east/h, because that type will be relatively more arable. This phenomenon is known as casualty switching.^[13]

Predator–casualty interaction [edit]

Predator–prey coevolution oft makes it unfavorable for a predator to swallow certain casualty items, since many anti-predator defenses increase treatment time.^[15] Examples include porcupine quills, the palatability and digestibility of the poison dart frog, crypsis, and other predator abstention behaviors. In improver, considering toxins may be present in many prey types, predators include a lot of variability in their diets to prevent whatsoever ane toxin from reaching unsafe levels. Thus, it is possible that an approach focusing only on energy intake may non fully explain an animal'south foraging beliefs in these situations.

The marginal value theorem and optimal foraging [edit]

Figure 3. Marginal value theorem shown graphically.

The marginal value theorem is a type of optimality model that is often practical to optimal foraging. This theorem is used to depict a situation in which an organism searching for food in a patch must determine when it is economically favorable to leave. While the animate being is within a patch, it experiences the law of diminishing returns, where information technology becomes harder and harder to notice prey as time goes on. This may be because the prey is being depleted, the casualty begins to accept evasive action and becomes harder to catch, or the predator starts crossing its own path more as it searches.^[4] This law of diminishing returns can be shown as a bend of energy proceeds per time spent in a patch (Figure three). The curve starts off with a steep slope and gradually levels off every bit prey becomes harder to find. Another important cost to consider is the traveling time between different patches and the nesting site. An animal loses foraging time while it travels and expends energy through its locomotion.^[ii]

In this model, the currency being optimized is commonly net free energy proceeds per unit time. The constraints are the travel time and the shape of the curve of diminishing returns. Graphically, the currency (net energy gain per unit time) is given by the slope of a diagonal line that starts at the offset of traveling time and intersects the bend of diminishing returns (Figure 3). In order to maximize the currency, i wants the line with the greatest slope that still touches the curve (the tangent line). The place that this line touches the bend provides the optimal conclusion dominion of the corporeality of time that the animate being should spend in a patch before leaving.

Examples of optimal foraging models in animals [edit]

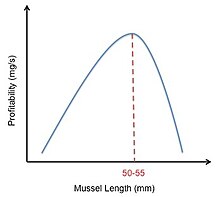
Effigy 4. Right-shifted mussel profitability curve. Adapted from Meire & Ervynck.^[16]

Optimal foraging of oystercatchers [edit]

Oystercatcher mussel feeding provides an example of how the optimal nutrition model can be utilized. Oystercatchers forage on mussels and crack them open with their bills. The constraints on these birds are the characteristics of the dissimilar mussel sizes. While large mussels provide more free energy than small mussels, large mussels are harder to crack open due to their thicker shells. This means that while large mussels have a higher energy content (Eastward), they also take a longer handling time (h). The profitability of any mussel is calculated as E/h. The oystercatchers must decide which mussel size volition provide plenty nutrition to outweigh the price and energy required to open it.^[2] In their study, Meire and Ervynck tried to model this conclusion past graphing the relative profitabilities of different sized mussels. They came up with a bell-shaped curve, indicating that moderately sized mussels were the virtually assisting. Withal, they observed that if an oystercatcher rejected as well many small mussels, the fourth dimension it took to search for the next suitable mussel greatly increased. This observation shifted their bong-curve to the correct (Figure 4). Nevertheless, while this model predicted that oystercatchers should prefer mussels of 50–55 mm, the observed data showed that oystercatchers actually prefer mussels of 30–45 mm. Meire and Ervynk then realized the preference of mussel size did not depend only on the profitability of the prey, just also on the prey density. After this was accounted for, they found a good agreement between the model's prediction and the observed data.^[16]

Optimal foraging in starlings [edit]

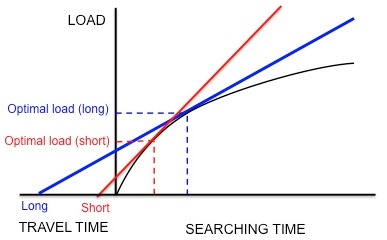
Figure 5. If starlings are maximizing net rate of free energy gain, longer traveling time results in larger optimum load. Adapted from Krebs and Davies.^[4]

The foraging behavior of the European starling, Sturnus vulgaris, provides an example of how marginal value theorem is used to model optimal foraging. Starlings leave their nests and travel to food patches in search for larval leatherjackets to bring dorsum to their young. The starlings must make up one's mind the optimal number of prey items to take back in one trip (i.e. the optimal load size). While the starlings forage inside a patch, they experience diminishing returns: the starling is able to hold simply so many leatherjackets in its neb, so the speed with which the parent picks up larvae decreases with the number of larvae that it already has in its pecker. Thus, the constraints are the shape of the curve of diminishing returns and the travel fourth dimension (the time information technology takes to brand a round trip from the nest to a patch and back). In addition, the currency is hypothesized to exist net energy gain per unit of measurement fourth dimension.^[four] Using this currency and the constraints, the optimal load can be predicted past drawing a line tangent to the bend of diminishing returns, every bit discussed previously (Figure 3).

Kacelnik et al. wanted to make up one's mind if this species does indeed optimize net free energy gain per unit of measurement time as hypothesized.^[17] They designed an experiment in which the starlings were trained to collect mealworms from an artificial feeder at different distances from the nest. The researchers artificially generated a fixed curve of diminishing returns for the birds by dropping mealworms at successively longer and longer intervals. The birds continued to collect mealworms as they were presented, until they reached an "optimal" load and flew home. Equally Figure v shows, if the starlings were maximizing net energy gain per unit time, a short travel time would predict a small optimal load and a long travel time would predict a larger optimal load. In agreement with these predictions, Kacelnik institute that the longer the altitude betwixt the nest and the artificial feeder, the larger the load size. In addition, the observed load sizes quantitatively corresponded very closely to the model'due south predictions. Other models based on dissimilar currencies, such as energy gained per energy spent (i.e. energy efficiency), failed to predict the observed load sizes every bit accurately. Thus, Kacelnik concluded that starlings maximize cyberspace energy gain per unit time. This determination was not disproved in later experiments.^{[xviii] [nineteen]}

Optimal foraging in bees [edit]

Worker bees provide another example of the use of marginal value theorem in modeling optimal foraging behavior. Bees forage from flower to blossom collecting nectar to carry dorsum to the hive. While this state of affairs is similar to that of the starlings, both the constraints and currency are really different for the bees.

A bee does not experience diminishing returns because of nectar depletion or any other characteristic of the flowers themselves. The full corporeality of nectar foraged increases linearly with time spent in a patch. Nevertheless, the weight of the nectar adds a significant cost to the bee'southward flight between flowers and its trip dorsum to the hive. Wolf and Schmid-Hempel showed, by experimentally placing varying weights on the backs of bees, that the price of heavy nectar is so great that information technology shortens the bees' lifespan.^[20] The shorter the lifespan of a worker bee, the less overall fourth dimension it has to contribute to its colony. Thus, there is a bend of diminishing returns for the internet yield of energy that the hive receives every bit the bee gathers more nectar during one trip.^[4]

The cost of heavy nectar as well impacts the currency used past the bees. Unlike the starlings in the previous case, bees maximize free energy efficiency (energy gained per energy spent) rather than cyberspace rate of free energy gain (net energy gained per fourth dimension). This is because the optimal load predicted by maximizing internet rate of energy gain is also heavy for the bees and shortens their lifespan, decreasing their overall productivity for the hive, as explained earlier. By maximizing energy efficiency, the bees are able to avert expending too much energy per trip and are able to live long enough to maximize their lifetime productivity for their hive.^[four] In a unlike newspaper, Schmid-Hempel showed that the observed human relationship between load size and flying fourth dimension is well correlated with the predictions based on maximizing energy efficiency, simply very poorly correlated with the predictions based on maximizing net rate of free energy gain.^[21]

Optimal foraging in Centrarchid Fishes [edit]

The nature of prey selection past two centrarchids (white crappie and bluegill) has been presented as a model incorporating optimal foraging strategies past Manatunge & Asaeda .^[22] The visual field of the foraging fish as represented by the reactive altitude was analysed in detail to estimate the number of prey encounters per search bout. The predicted reactive distances were compared with experimental data. The energetic toll associated with fish foraging behaviour was calculated based on the sequence of events that takes place for each prey consumed. Comparisons of the relative abundance of casualty species and size categories in the tum to the lake environment indicated that both white crappie and bluegill (length < 100 mm) strongly select prey utilizing an energy optimization strategy. In most cases, the fish exclusively selected large Daphnia ignoring evasive prey types (Cyclops, Diaptomids) and small cladocera. This selectivity is the consequence of fish actively avoiding casualty with loftier evasion capabilities even though they appear to be high in energetic content and having translated this into optimal selectivity through capture success rates. The energy consideration and visual system, apart from the forager'due south ability to capture prey, are the major determinants of prey selectivity for large-sized bluegill and white crappie still at planktivorous stages.

Criticism and limitations of the optimal foraging theory [edit]

Although many studies, such every bit the ones cited in the examples in a higher place, provide quantitative back up for optimal foraging theory and demonstrate its usefulness, the model has received criticism regarding its validity and limitations.

Commencement, optimal foraging theory relies on the assumption that natural selection volition optimize foraging strategies of organisms. However, natural selection is not an anointed strength that produces perfect designs, but rather a passive procedure of option for genetically-based traits that increase organisms' reproductive success. Given that genetics involves interactions betwixt loci, recombination, and other complexities, there is no guarantee that natural selection can optimize a specific behavioral parameter.^[23]

In addition, Oft likewise assumes that foraging behaviors are able to exist freely shaped past natural choice, because these behaviors are independent from other activities of the organism.^[23] However, given that organisms are integrated systems, rather than mechanical aggregates of parts, this is non always the example. For example, the need to avoid predators may constrain foragers to feed less than the optimal charge per unit. Thus, an organism'due south foraging behaviors may not be optimized every bit OFT would predict, because they are not independent from other behaviors.^[24]

Some other limitation of OFT is that it lacks precision in practice. In theory, an optimal foraging model gives researchers specific, quantitative predictions most a predator's optimal conclusion rule based on the hypotheses most the currency and constraints of the system. However, in reality, it is difficult to ascertain bones concepts like prey type, meet rates, or fifty-fifty a patch as the forager perceives them.^[23] Thus, while the variables of OFT can seem consequent theoretically, in exercise, they can be arbitrary and difficult to measure out.

Furthermore, although the premise of Frequently is to maximize an organism's fettle, many studies testify only correlations between observed and predicted foraging behavior and end curt of testing whether the animal's behavior really increases its reproductive fitness. It is possible that in certain cases, there is no correlation betwixt foraging returns and reproductive success at all.^[23] Without accounting for this possibility, many studies using the Oft remain incomplete and neglect to address and examination the main point of the theory.

One of the about imperative critiques of OFT is that information technology may not be truly testable. This issue arises whenever at that place is a discrepancy between the model'southward predictions and the actual observations. Information technology is difficult to tell whether the model is fundamentally incorrect or whether a specific variable has been inaccurately identified or left out. Because information technology is possible to add endless plausible modifications to the model, the model of optimality may never exist rejected.^[23] This creates the trouble of researchers shaping their model to fit their observations, rather than rigorously testing their hypotheses about the animal's foraging beliefs.

References [edit]

1. ^ Werner, E. East.; Hall, D. J. (1974). "Optimal Foraging and the Size Selection of Prey by the Bluegill Sunfish (Lepomis macrochirus)". Environmental. 55 (5): 1042. doi:10.2307/1940354. JSTOR 1940354.
2. ^ ^{a b c d e f g h} Sinervo, Barry (1997). "Optimal Foraging Theory: Constraints and Cognitive Processes" Archived 23 November 2015 at the Wayback Machine, pp. 105–130 in Behavioral Ecology. University of California, Santa Cruz.
3. ^ Stephens, D. Due west. and Krebs, J. R. (1986) "Foraging Theory". 1st ed. Monographs in Behavior and Ecology. Princeton University Press. ISBN 9780691084428.^{[ page needed ]}
4. ^ ^{a b c d e f k h i j k l m} Krebs, J. R. and Davies, N. B. (1989) An Introduction to Behavioral Ecology. 4th ed. Oxford: Blackwell Scientific Publications.^{[ ISBN missing ] [ folio needed ]}
5. ^ Verlinden, C.; Wiley, R. H. (1989). "The constraints of digestive rate: An alternative model of diet option". Evolutionary Ecology. 3 (3): 264. doi:10.1007/BF02270727. S2CID 46608348.
6. ^ ^{a b} Parker, G. A.; Smith, J. G. (1990). "Optimality theory in evolutionary biology". Nature. 348 (6296): 27. Bibcode:1990Natur.348...27P. doi:10.1038/348027a0.
7. ^ Cortés, E.; Gruber, S. H.; Cortes, E. (1990). "Diet, Feeding Habits and Estimates of Daily Ration of Young Lemon Sharks, Negaprion brevirostris (Poey)". Copeia. 1990 (1): 204–218. doi:10.2307/1445836. JSTOR 1445836.
8. ^ Godfray, H. C. J. (1994) Parasitoids: Behavioral and Evolutionary Ecology. Princeton Academy Press, Princeton.^{[ ISBN missing ] [ page needed ]}
9. ^ Stephens, D.W., Brown, J.S., and Ydenberg, R.C. (2007). Foraging: Behavior and Ecology. Chicago: University of Chicago Press.^{[ ISBN missing ] [ page needed ]}
10. ^ ^{a b} Pulliam, H. Ronald (1974). "On the theory of optimal diets". American Naturalist. 108 (959): 59–74. doi:x.1086/282885. JSTOR 2459736. S2CID 8420787.
11. ^ Adler, 1000. H.; Wilson, G. L. (1987). "Demography of a Habitat Generalist, the White-Footed Mouse, in a Heterogeneous Environment". Ecology. 68 (half-dozen): 1785–1796. doi:10.2307/1939870. JSTOR 1939870. PMID 29357183.
12. ^ Shipley, L. A.; Forbey, J. S.; Moore, B. D. (2009). "Revisiting the dietary niche: When is a mammalian plant eater a specialist?". Integrative and Comparative Biology. 49 (three): 274–290. doi:ten.1093/icb/icp051. PMID 21665820.
13. ^ ^{a b c d e} Staddon, J.Eastward.R. "Foraging and Behavioral Environmental." Adaptive Behavior and Learning. Commencement Edition ed. Cambridge UP, 1983.^{[ ISBN missing ] [ page needed ]}
14. ^ ^{a b} Jeschke, J. M.; Kopp, M.; Tollrian, R. (2002). "Predator Functional Responses: Discriminating Betwixt Treatment and Digesting Prey". Ecological Monographs. 72: 95–112. doi:ten.1890/0012-9615(2002)072[0095:PFRDBH]2.0.CO;2.
15. ^ Boulding, Elizabeth Grace (1984). "Crab-resistant features of shells of burrowing bivalves: decreasing vulnerability by increasing handling time". Journal of Experimental Marine Biology and Ecology. 76 (3): 201–23. doi:10.1016/0022-0981(84)90189-eight.
16. ^ ^{a b} Meire, P. M.; Ervynck, A. (1986). "Are oystercatchers (Haematopus ostralegus) selecting the almost profitable mussels (Mytilus edulis)?" (PDF). Beast Behaviour. 34 (five): 1427. doi:ten.1016/S0003-3472(86)80213-five. S2CID 53705917.
17. ^ Kacelnik, A. (1984). "Central Place Foraging in Starlings (Sturnus vulgaris). I. Patch Residence Time". The Journal of Animal Ecology. 53 (1): 283–299. doi:10.2307/4357. JSTOR 4357.
18. ^ Bautista, Fifty.M.; Tinbergen, J.M.; Wiersma, P.; Kacelnik, A. (1998). "Optimal foraging and across: how starlings cope with changes in food availability" (PDF). The American Naturalist. 152 (4): 221–38. doi:10.1086/286189. hdl:11370/1da2080d-6747-4072-93bc-d761276ca5c0. JSTOR 10.1086/286189. PMID 18811363. S2CID 12049476.
19. ^ Bautista, Fifty.M.; Tinbergen, J.K.; Kacelnik, A. (2001). "To walk or to wing? How birds choose among foraging modes". Proc. Natl. Acad. Sci. USA. 98 (iii): 1089–94. Bibcode:2001PNAS...98.1089B. doi:10.1073/pnas.98.3.1089. JSTOR 3054826. PMC14713. PMID 11158599.
20. ^ Wolf, T. J.; Schmid-Hempel, P. (1989). "Extra Loads and Foraging Life Span in Honeybee Workers". The Journal of Animal Ecology. 58 (3): 943. doi:10.2307/5134. JSTOR 5134.
21. ^ Schmid-Hempel, P.; Kacelnik, A.; Houston, A. I. (1985). "Honeybees maximize efficiency by not filling their crop". Behavioral Ecology and Sociobiology. 17: 61–66. doi:10.1007/BF00299430. S2CID 23423388.
22. ^ Manatunge, Jagath; Asaeda, Takashi (1998). "Optimal foraging as the criteria of prey option by ii centrarchid fishes". Hydrobiologia. 391 (1): 221–39. doi:10.1023/a:1003519402917. S2CID 24808827.
23. ^ ^{a b c d e} Gray, Russell D. "Faith and Foraging: A Critique of the "Paradigm Statement from Design"" p. 198 in Foraging Behavior. Ed. Alan C. Kamil, John R. Krebs, and H. Robald Pulliam. New York: Plenum^{[ ISBN missing ]}
24. ^ Pierce, M. J.; Ollason, J. Grand. (1987). "Eight reasons why optimal foraging theory is a complete waste product of time" (PDF). Oikos. 49 (one): 111–eighteen. doi:ten.2307/3565560. JSTOR 3565560.

Further reading [edit]

• Optimal Foraging Theory by Barry Sinervo (1997), Form: "Behavioral Environmental 2013", Department of Ecology and Evolutionary Biology, UCSC – This Section, of that Course at UCSC, considers OFT and 'Adaptational Hypotheses' ('guided trial and error, instinct'). forth with addition subjects such equally "Casualty Size", "Patch Residence Time", "Patch Quality and Competitors", "Search Strategies", "Risk Aversive Behavior" and foraging practices subject to "Food Limitation". Come across also: up one Level for the Primary Section of the Class, where downloadable PDFs are available (every bit the Images on that Folio seem broken currently). The PDF for the above Link is 26 Pages long (with Images).

Source: https://en.wikipedia.org/wiki/Optimal_foraging_theory

Posted by: collinscapon1936.blogspot.com

Share this post